Рассмотрим прогноз ряда месячных данных по числу пассажиров международных авиалиний (airlines.dat). Возьмем за основу первые 120 точек ряда, чтобы иметь возможность оценивать качество построенного прогноза (рис.1).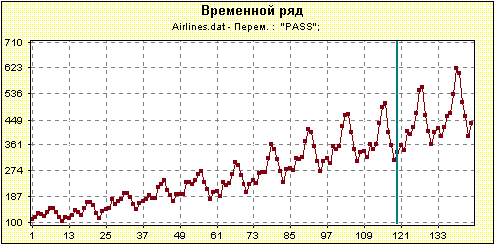

Рис.1. Ежемесячные данные по числу пассажиров международных авиалиний (в тысячах). Прогноз будет строиться на основе первых 120 точек.

На рис.2 изображены комплексные корни характеристического полинома, соответствующего выбору первых 17 главных компонент. Ось X соответствует вещественной части корня, а ось Y - его мнимой части. Количество корней совпадает с длиной гусеницы (в данном случае их 60).

Пара корней с одинаковой ненулевой вещественной частью и противоположными по знаку мнимыми частями соответствует синусоидальной составляющей ряда с амплитудой, меняющейся по экспоненте. Причем, если модуль корня больше единицы, то амплитуда возрастает, а если меньше 1, то она убывает. Модуль, равный единице, показывает постоянство амплитуды. Период синуса равен 2*p, деленному на величину угла между осью X и лучом, проходящим через точку корня. Таким образом, есть возможность определять периоды по корням характеристического полинома.

Вещественные положительные корни соответствуют тренду. Корень кратности 2, лежащий на единичной окружности, соответствует линейному тренду. Корень, лежащий вне единичного круга, соответствует возрастающей экспоненте, внутри - убывающей.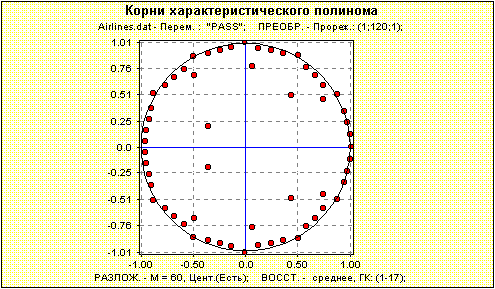

Рис.2. Комплексные корни характеристического полинома, соответствующего выбору первых 17 ГК.

На рис.3 изображен прогноз на 24 точки вперед ряда, выбранного нами в качестве базового. Видно, что прогноз несколько завышен. Поэтому возникает желание несколько "подправить" его.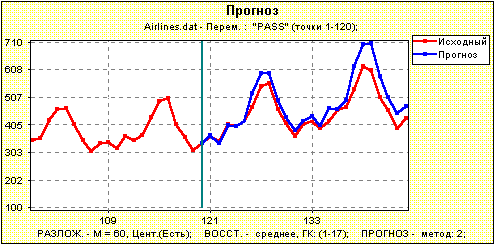

Рис.3. Прогноз по рекуррентной формуле, порождающей характеристический полином с корнями, изображенными на рис.2.

Длина гусеницы как правило гораздо больше, чем размерность ряда (имеется ввиду аппроксимирующий ряд). Поэтому часть корней соответствует слагаемым, которые или не влияют на поведение ряда (в лучшем случае), или портят его поведение, добавляя ложные слагаемые. В данном случае очевидно ряд состоит из растущего тренда и 12-месячной периодики. Тем самым, интерпретируемыми являются вещественные положительные корни, лежащие вне единичной окружности, и комплексные корни, соответствующие периодам 12, 6=12/2, 4=12/3, 3=12/4, 2.4=12/5 и 2=12/6. Видно, что период 2 отсутствует, а все остальные корни лежат вне единичной окружности (амплитуда 12-месячной периодики действительно возрастает).

Сделаем следующие шаги: уберем все неинтерпретируемые корни и подправим корни, порожденные периодикой 12, используя знания о точных значениях периодов. Результат изображен на рис.4.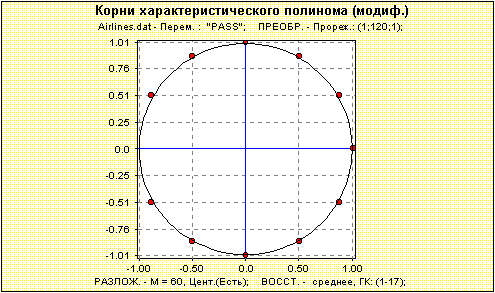

Рис.4. Интерпретируемые корни, соответствующие тренду и 12-месячной периодике.

На рис.5 изображен прогноз по рекуррентной формуле, порождающей характеристический полином с корнями, изображенными на рис.4.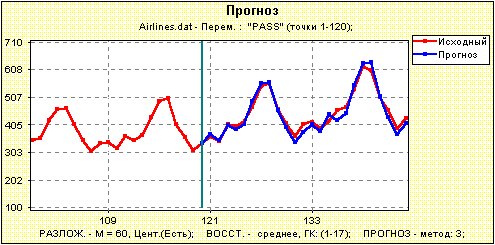

Рис.5. Прогноз по рекуррентной формуле, порождающей характеристический полином с корнями, изображенными на рис.4.

Во-первых, видно, что прогноз более точен. Во-вторых, его поведение описывается конечным числом интерпретируемых слагаемых.

См. также: Прогноз с доверительными интервалами